Periodische Stempelzahlfolgen
Zahlenfolgen sind mathematische Strukturen,
die beginnend bei einem Anfangswert mithilfe eines Bildungsgesetzes Zahlen einer Menge in Beziehung setzen und verketten.
Das Interessante an den hier gezeigten Folgen ist ihre periodische Struktur
und im Bildungsgesetz die Verknüpfung von Zweierpotenzen mit Primfakultäten.
Zuerst brauchen wir nur eine Definition und einige Eigenschaften der Stempelzahlen.
(Stempelzahlen ist hier nur ein Arbeitsbegriff, der bekannte Sätze und Gegebenheiten zusammenfasst.)
Sei G (für GGT-Menge) die Menge aller natürlichen teilerfremden Zahlen z (kleiner als eine Grenzzahl g).
Es gilt also: GGT(z, g) = 1 (mit z<g)
Eine Stempelzahlmenge S ist eine G Menge, also die Menge aller zu einer Obergrenze teilerfremden Zahlen,
mit einer Primfakultät mi als Obergrenze
(einem Produkt aufeinander folgender Primzahlen beginnend bei 2: 2, 6,30,210,2310,30010, …).
Wichtig ist die Symmetrie der Stempelzahlen:
Satz 1: Sei s1 eine Stempelzahl, so ist s2 = mi - s1 auch ein Element der Menge S.
(s2 ist teilerfremd zu mi, da s1 keinen Teiler von mi enthält.)
Die Hälfte von mi h= mi/2 ist für die folgenden Überlegungen ebenfalls von großer Bedeutung.
Sie enthält außer der 2 alle Faktoren von mi.
Beispiele für die Stempelzahlgrenze 210:
h=105 103+107=210 . . . 199+11=210
Abstandssatz
Es gilt nun folgender Abstandssatz, der die Grundlage der Stempelzahlfolgen bildet:
Satz 2: Jede Stempelzahl s oder jedes Element von S hat zu h den Abstand 2k * s1,
wobei s1 wiederum ein Element von S ist und k>0.
s = h +/- 2k * s1
Der Beweis des Abstandssatzes
Der Satz besagt, dass s einen Abstand zu h hat, der größer als Null ist,
mindestens durch zwei teilbar ist und sofern er nicht eine reine Zweierpotenz ist,
als weiteren Faktor eine ebenfalls zu mi teilerfremde Zahl enthält.
Dies kann man einzeln beweisen:
Es gilt: s, h und 2 sind alle paarweise teilerfremd.
h ist ungleich s, da sonst nicht teilerfremd zu mi und damit ist der Abstand größer als 0.
Da h wie s ungerade ist, muss der Abstand zwischen ihnen mindestens durch zwei teilbar sein.
Die Zahl s1 gibt alle Zweierfaktoren an 2k ab und ist selbst ungerade.
Falls s1 ungleich 1 ist, muss es wegen s zu h teilerfremd sein, ist damit zu mi teilerfremd
und damit ein Element der Menge S.
Spezialfälle des Abstandsatzes
Verdoppelt man obige Formel und setzt s1=1:
2*s = mi +/- 2(k+1) * s1
Dann ergibt sich, dass mi plus/minus einer Zweierpotenz (>2) immer das Doppelte einer Stempelzahl ergibt.
(30 +/- 4/8/16 oder 210 +/- 4/8/16/32/64)
Erhöht man die Potenzen der Faktoren von h und sucht wieder im Abstand von Zweierpotenzen finden sich weitere zu mi teilerfremde Zahlen (>mi).
(3h: 45 +/- 2/(4)/8/16 5h: 75 +/- (2)/4/8)
Die Viertelsymmetrie
Aus dem Abstandsatz folgt zuerst einmal, dass s1 < h/2 = mi /4 ist.
Aus allen Stempelzahlen des unteren Viertels und den Zweierpotenzen lassen sich also alle anderen Elemente der Menge S darstellen.
Dafür werden anderseits auch alle Elemente des unteren Viertels und alle Zweierpotenzen gebraucht.
Es gibt keine Zweierpotenz und kein Produkt (2n * s1)<h, dass nicht zu einer Stempelzahl führt
und keine Stempelzahl, die nicht so dargestellt werden kann.
Jede Stempelzahl kann so (neben ihrer symmetrischen Spiegelzahl) auf eine weitere Stempelzahl kleiner mi/4 abgebildet werden.
Aufbau einer Stempelzahlenfolge
Die im Abstandssatz enthaltene Stempelzahl s1 kann selbst wieder mithilfe des Abstandssatzes dargestellt werden.
s1 = h - 2l * s2 (s1 <h/2)
s1 kann dabei unmöglich gleich s2 sein, da sonst h durch s1 teilbar sein müsste.
(Es ist daher keine Folge mit der Länge 1 möglich, Zu den Sonderfällen der ersten Stempel siehe unten.)
s1, s2 und alle weiteren Folgeglieder sind dabei immer kleiner als mi/4.
Alle Stempelzahlen >mi/4 werden nie von Elementen <mi/4 aus erreicht,
sondern bilden Einstiegsfolgen der Länge 1 oder Einstiegselemente zu periodischen Folgen aus Elementen <mi/4.
Die Endlichkeit der Stempelzahlfolgen
Da die Stempelzahlen eine endliche Zahlenmenge darstellen, muss jede Stempelzahlenfolge nach n Schritten auf ein bereits vorhandenes Element stoßen.
Die Folge wird dadurch für Elemente <mi/4 immer periodisch. (vgl. Folgen von Teilbarkeitsresten)
Jedem Element <m/4 sind je nach Anzahl der mit diesem Element kombinierbaren Zweierpotenzen
entsprechend viele Einstiegselemente >mi/4 zugeordnet.
Die Kreisstruktur der Folgeglieder kleiner m/4
Für alle Elemente kleiner m/4 gilt:
Jedes Element hat genau einen Vorgänger und einen Nachfolger, der auch kleiner m/4 ist.
Jedes Element ist immer Teil eines und genau eines geschlossenen Rings aus Elementen kleiner m/4.
Alle Elemente kleiner m/4 gliedern sich damit in disjunkte Teilmengen oder ringförmige Zahlenfolgen.
Jeder Ring hat ein kleinstes Element e. Damit lassen sich alle Einstiegselemente und alle Kreiselemente oder einfach alle Stempelzahlen der Menge S so darstellen:
s=|(2n+1)*h - e*2^x|
Werden zwei Elemente multipliziert, ist das Produkt nicht mehr Element desselben Rings, ausser e=1 für einen oder beide Faktoren.
Die Einstiegselemente und Folgen
Auch die Elemente von S grösser als m/4 gruppieren sich eindeutig. Ein oder mehrere solcher Elemente haben dasselbe Folgeelement kleiner m/4.
Die Anzahl x der Elemente einer Einstiegsfolge hängt von der Grösse des Einstiegselementes ab. Mit welcher maximalen Zweierpotenz kann es multipliziert werden, bevor das Produkt grösser h wird.
h - 2^x *e >0
Die Anzahl x ist damit der gerundete Zweierlogarithmus von h/e. Für jede Zweierpotenz ergeben sich plus/minus h zwei Einstiegselemente.
Die Basisfolge
Da die 1 ein Element jeder Stempelzahlenmenge S ist, beginnt mit dieser Stempelzahl die Basisfolge
und endet mit der ersten reinen Zweierpotenz, die wieder die 1 liefert:
sn = h - 2n * 1
Diese Zweierpotenz muss zwischen mi/4 und mi/2 liegen.
Da es zwischen einer Zahl und ihrem Doppelten immer eine und nur eine Zweierpotenz gibt,
(falls diese Zahl nicht selbst eine Zweierpotenz ist),
gibt es nur eine Stempelzahlfolge, die mit der 1 endet. Alle anderen Zweierpotenzen führen zu Einstiegselementen dieser Folge,
da die korrespondierende Stempelzahl >mi/4 ist.
Der 1 in der Basisfolge sind daher am meisten Einstiegselemente und genau ein Vorgängerelement (<mi/4) zugeordnet.
Für alle Elemente der Basisfolge gilt: Sie sind von einem Vielfachen von h nur eine Zweierpotenz entfernt.
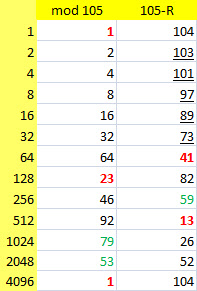
Zur Verdeutlichung hier die Basisfolge von 210 (1, 13, 23, 41, 1) und die Umrechnung in Vielfache von h und Zweierpotenzen:
1 = h- 8*(h - 4*(h - 2*(h −2^6)))
41 = h- 64
23 = 2^7 -h
13 = 5h - 2^9
1 = 2^12 - 39h
Betrachtet man die Reste von h mod aufsteigender Zweierpotenzen, so ist die Basisfolge daraus eine Auswahl der ungeraden Reste < mi/4 und auch alle anderen Einstiegselemente von Zweierpotenzen oder von anderen Stempelzahlen kommen als Reste vor, keine weiteren ungeraden Zahlen.
Beispiel 105:
Die ersten Stempelzahlfolgen
Für mi=2 mit h=1 ergibt sich noch keine Folge.
Für mi=6 mit h=3 erhält man als erste Folge die 1 mit der 5 als Einstiegselement.
Für mi=30 mit h=1 ergibt sich die Folge (1, 7).
Einstiegselemente zur 1 sind die Elemente 11, 13, 17, 19, 23
und zur 7 das Element 29.
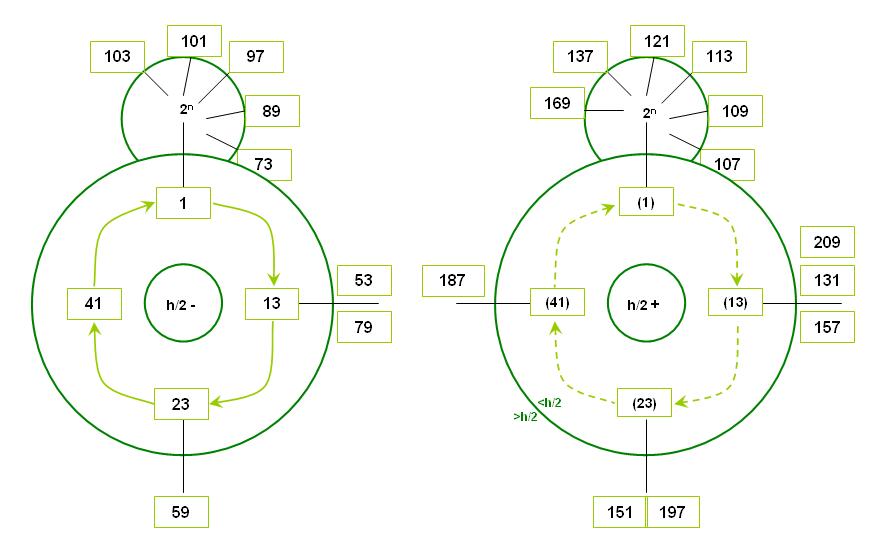
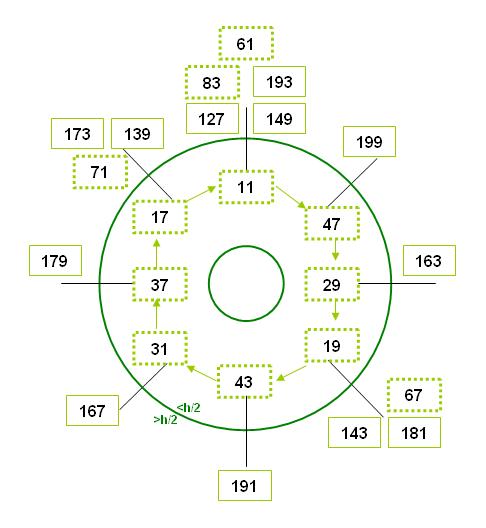
Die Menge S zu mi=210 umfasst 48 Elemente, 12 davon sind kleiner als 52,5.
Sie teilen sich in zwei Folgen auf, beginnend mit der 1 und der 11.
4 Elemente: 1 13 23 41 1
8 Elemente: 11 47 29 19 43 31 37 17 11
Die Menge S zu mi=2310 umfasst 480 Elemente, 120 davon sind kleiner als 577,5.
Sie teilen sich in vier Folgen auf, beginnend mit den Zahlen 1, 13, 17 und der 19.
32 Elemente:
1 577 289 433 361 397 379 97 529 313 421 367 197 479 169 493
331 103 263 223 233 461 347 101 527 157 499 41 557 299 107 131 1
28 Elemente:
13 571 73 541 307 53 551 151 251 113 521 317 419 23 283 109
523 79 269 443 89 533 311 211 59 137 509 323 13
28 Elemente:
17 569 293 431 181 487 167 247 227 29 563 37 559 149 503 163
31 281 437 359 199 239 229 463 173 491 83 67 17
32 Elemente:
19 71 271 221 467 43 139 127 257 449 353 401 377 389 383 193 481
337 409 373 391 191 241 457 349 403 47 277 439 179 61 547 19
In der Menge S zur Primfakultät 30030 finden sich bei 2880 Elementen bereits 48 Folgen,
die (ohne Einstiegselemente) nie mehr als 34 Elemente enthalten.
Hier die Basisfolge:
1, 7507, 1877, 6569, 4223, 1349, 6833, 4091, 2731, 3071, 1493, 6761, 4127, 1361, 6827, 2047, 1621, 6697, 4159, 1357, 6829, 4093, 5461, 4777, 5119, 1237, 6889, 4063, 1369, 6823
Für die Stempelgröße 210 ist hier die Basisfolge und die einzige weitere Folge (beginnend mit der 11) dargestellt.
Besonderheiten der Stempelzahlfolgen
Die Summe aller Stempelzahlen kleiner h im Abstand einer Zweierpotenz lässt sich allgemein berechnen.
Sei n die höchste Zweierpotenz kleiner h, so ist die Summe A dieser Zahlen:
A= n*h - 2n+1 +2
Ausbreitung und Vernetzung der Folgen
(Wie werden die Glieder einer Folge auf die Folgen der nachfolgenden Stempelzahlmenge verteilt?)
Welches Maximum hat das Auftauchen mindestens eines Elementes jeder Folge.
Summe der Kehrwerte der Basisfolge (tendiert gegen 1).
Variationen der Folgen
(k*h als Ausgangspunkt)
Bedeutung der Stempelzahlfolgen
(Vielleicht lassen sich damit schwache Primzahlen ermitteln und bei der Erzeugung von Zertifikaten ausschließen.)