• Druckansicht

Stempelzahlen

    * 1 Die mathematische Darstellung der Stempelzahlen
    * 2 Eigenschaften der Stempelzahlen
    * 3 Anzahl und Dichte der Stempelzahlen
    * 4 Beispiele
    * 5 Stempelzahlprodukte
    * 6 Stempelzahlvermutungen
    * 7 Weitere Ideen
    * 8 Anmerkungen
    * 9 Siehe auch
    * 10 Weblinks

    * 11 Periodische Stempelzahlfolgen

Der Begriff Stempelzahlen entstand als Arbeitsbegriff für primzahlenähnliche Zahlengruppen, die nach teilweise durchgeführten Siebverfahren (Ulam, Eratosthenes) neben einer hohen Dichte an Primzahlen noch aus großen Faktoren zusammengesetzte Zahlen enthalten. Der Begriff des Stempels findet sich im hier verwendetem Sinn bereits bei dem polnischen Mathematiker Stanisław Marcin Ulam. Das nette an den Stempelzahlen ist, dass man mit ihnen viele mathematische Themen anschaulich durchspielen kann (Resteklassen, ...).

Einfachste Definition:
Sei G (für GGT-Menge) die Menge aller teilerfremden Zahlen z kleiner als eine Grenzzahl g, für die damit gilt: GGT(z, g) = 1 (mit z<g)
Die Stempelzahlen sind alle GGT-Mengen, also der zu einer Obergrenze teilerfremden Zahlen, mit einem Primorial als Obergrenze (einem Produkt aufeinanderfolgender Primzahlen beginnend bei 2: 2, 6,30,210,2310,30010, ....).

Definition als Stempelmenge
Stempelzahlen sind natürliche Zahlen, die aus zwei teilerfremden Komponenten (Vielfachen des nächstkleineren Primorials und Stempelzahlen dieses kleineren Bereichs) zusammengesetzt sind. Sie entstehen durch den Sieb des Ulam. Die Basis bildet ein Vielfaches eines Primorial m, das aus aufeinander folgenden Primfaktoren zusammengesetzt ist (2, 2*3, 2*3*5, ... Primfakultät kleiner gleich n). Das größte erlaubte Vielfache von m ist um 1 kleiner als der größte m-Faktor (4*6 +5=29 oder 6*30+29=209). Zur Basis werden die teilerfremden Elemente kleinerer Stempel addiert (und Vielfache des größten m-Faktors gestrichen: 5 und 25 im 30er Stempel, 7,77,... im Bereich bis 210). So entstehen Stempelbereiche, die alle Stempelzahlen kleiner m enthalten und der Ausgangsstempel für den nächsthöheren Bereich sind.

Definition als Zahlensystem
Stempelzahlen lassen sich als Zahlensystem ähnlich dem Dualsystem oder Dezimalsystem verstehen. Statt der Potenzen von 2 oder 10 werden hier immer größer werdende Produkte aufeinander folgender Primzahlen verwendet.

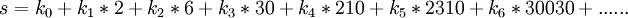
Ferner gilt, k₀ = 1, dass die k-Koeffizienten nur die Größe 0 bis (größter m-Faktor -1) haben dürfen und dass jede Summe aller Summanden links zu jeder aller Summanden rechts eines Pluszeichens teilerfremd ist!

Die Addition eines Vielfachen einer höheren m-Ebene bewirkt das Stempeln und die Bedingung teilerfremd bewirkt das Streichen von Vielfachen des Teilers dieser m-Ebene! Im Ergebnis enthält ein Stempel einfach alle zur Stempelgröße m teilerfremden Zahlen kleiner m. Er fasst das Teilbarkeitsverhalten in Bezug auf die Stempelgröße zusammen. (vgl. Sieb des Eratosthenes und Sieb des Ulam)

Stempel können beliebig um das k-fache ihrer Stempelgröße verschoben werden. Sie werden dabei immer nach oben verschoben. Am neuen Platz finden sich uU weniger Stempelzahlen durch Streichungen, nie mehr. Außer an den Plätzen ihres Stempels gibt es auch an der neuen Stelle keine Stempelzahlen. Auch am neuen Platz fasst der Stempel das Teilbarkeitsverhalten bezogen auf seine Stempelgröße zusammen.

Der kleinste Stempel ist der m-Bereich 2 und enthält nur die 1. Der nächste enthält mit m=6 die Zahlen 1 und 5. Er besteht aus 3 2er Stempeln. Die 3 wird als Vielfaches des aktuellen m-Faktors 3 sofort gestrichen. Der dritte Stempel aus 5 Stempeln des 6er Bereichs ist der 30er Bereich mit den Elementen 1,7,11,13,17,19,23,29. Die Zahlen 5 und 25 werden gestrichen. 7 Stempel des 30er Bereichs ergeben den 210er Stempel. Hier werden bereits 8 Vielfache von 7 gestrichen. (91 und 119 symmetrisch im selben mittleren 30er Stempel.) Jede größere Zahl liegt in einem 30er, 210er, ... Stempelbereich und hat durch diese Position charakteristische Resteklassen.

Die mathematische Darstellung der Stempelzahlen

Eigenschaften der Stempelzahlen

Symmetrie:
Die Stempelzahlen sind symmetrisch zur jeweiligen Bereichsmitte m/2: Ist s₁ eine Stempelzahl des Bereichs m_i, dann ist die Spiegelzahl s₂ = m_i-s₁ ebenfalls ein Element dieses Bereichs. (Streichungen erfolgen ebenfalls symmetrisch.)
Symmetrisch sind auch alle Lücken und alle Stempelzahlenzwilling. Die Lücken kleinerer Stempel vervielfältigen sich und werden durch symmetrische Streichungen vergrößert.

Anzahl und Summe:
Die Anzahl der Stempelzahlzwillinge wächst etwas schwächer, aber in derselben Stärke wie die Anzahl der Stempelzahlen. Die Anzahl der Produkte oder nicht-primen Stempelzahlen wächst stärker als die Anzahl der Stempelzahlen.

Die Summe aller Stempelzahlen eines Bereichs ist ein Vielfaches von m. (Aufgrund der Symmetrie das m-fache der Hälfte der Anzahl für diesen Bereich)

Abstände und Zweierpotenzen
Die geraden Abstände 2*d von s zur Bereichsmitte m/2 sind entweder Potenzen von 2 oder Kombinationen von Stempelzahlen s1 mit Potenzen von 2. Da man s1 wieder genauso zerlegen kann, lässt sich jede Stempelzahl durch Zweierpotenzvielfache von Bereichsmitten darstellen.
s= mi/2 +/- 2^a *s1 = mi/2 +/- 2^a * (mj/2 +/- 2^b *s2)
151 = 105 + 2* 23 = 105 + 2*15 + 2*8
Zweierpotenzen selbst haben eine enge Beziehung zu m/2 bzw. 30/2=15 = (4-1)*(4+1)=16-1
2^n = 2^(n-4) * (15+1) = 2^(n-5) * 30 + 2^(n-4)
Die Addition einer Zweierpotenz verschiebt eine Stempelzahl in einen anderen 30 er Stempel und darin um eine kleine Zweierpotenz (2^(n-4) lässt sich ja wieder zerlegen ...)
Noch anders ausgedrückt, befindet sich zu jeder Stempelzahl im Abstand großer Zweierpotenzen ein Vielfaches von 15 und von dort aus lassen sich mit Zweierpotenzen wieder Stempelzahlen erreichen.
Das liegt daran, dass Zweierpotenzen mod 15 die Reste 1,2,4,8 haben und
Stempelzahlen mod 15 dieselben plus deren negative Spiegelung 1/16, -8/7, -4/11, -2/13, 2,17, 4/19, 8/23, -1/-16/29
29 + 16 = 45 45+16=61
Hinzu kommt, dass Zweierpotenzen durch Vielfache von 30 zu grösseren Zweierpotenzen erweitert werden können.
240+16=256. 29+32=61
29 +256 =285 285+256=541. 29+512=541
Jede Stempelzahl lässt sich daher in der Form s= k*15 +/- 2^n. darstellen.
In jedem Stempel mit mi>6 gibt es zu jeder Stempelzahl ein maximales n.

Es gilt folgender Abstandssatz:
Jede Stempelzahl eines Bereichs mi lässt sich in der Form s= hi +/- s1*2^n (mit hi =mi/2 , s1*2^n < hi , s1 < mi/4 , GGT(s,hi)=1 und GGT(s,s1)=1) darstellen. (Beweis siehe hier)
Eine Stempelzahl ist um das Zweierpotenzvielfache einer kleineren Stempelzahl s1 von ihrer Bereichsmitte hi entfernt.
817 = 1155-2*169
Alle Stempelzahlen kleiner mi/4 sind kombiniert mit den 2er-Potenzen in der Lage alle Stempelzahlen eines Bereichs darzustellen.
Daraus folgt, dass jede Stempelzahl und damit jede Primzahl aus Bereichsmitten und Zweierpotenzen kombiniert werden kann.
Dies ergibt eine weitere Darstellung der Stempelzahlen:
31 = 105-2*37 = 105 -2*(105-4*17) = 105 -2*(105-4*(15+2))

Umgekehrt gilt auch dass jede Zweierpotenz von der nächst größeren Bereichsmitte genau eine Stempelzahl entfernt ist oder die Subtraktion einer Zweierpotenz (>2) von einer Primfakultät immer das Doppelte einer Stempelzahl ergibt.
2*s= mi - 2^(n+1)

Auf diese Weise lassen sich auch eigene Gruppen von Stempelzahlen definieren.
Zum Beispiel bilden die Stempelzahlen eines Bereichs im Abstand einer Zweierpotenz zur Mitte eine eigene Klasse
41 73 89 97 101 103
169 137 121 113 109 107
Die Summe dieser Prim- oder Stempelzahlen(?), deren Differenz zu einer Zweierpotenz führt, ergibt sich als:
6*105 - (2+4+8 …64) =5*126 −126 = 504 = 4*126
6*15 -(2+4+8) = 76 =4*19
allgemein: n*hi - 2^(n+1) +2

Auch alle Zahlen der Form s =2^n*s1*s2*s3*... +/-1 (2*11 +1 =23)
oder der Form s =s1*s2*s3*... +/-2^n (3*7 -2 = 19) kann man gruppieren.
(So entstehen allerdings nicht immer nur Stempelzahlen!)

Nebenbei ist die um 1 verminderte (erhöhte) Bereichsmitte immer ein Zweierpotenzvielfaches einer Stempelzahl (oder wie bei 16 eine Zweierpotenz) und nicht nur bloß das Doppelte einer Stempelzahl.
15-1 = 2*7 16 = 2^4 104=8*13 106=2*53

Beziehungsstrukturen der Stempelzahlen und Resteverhalten
Zu jeder Stempelzahl existieren verwandte Stempelzahlen im Abstand 2^n,2 * 3^n, zu bestimmten auch im Abstand anderer Potenzen (resteabhängig). Dabei folgen nie dieselben Potenzen direkt hintereinander ((23+8)+16=(31)+16=47).

Mod m werden Stempelzahlprodukte eines Bereichs wieder auf Stempelzahlen dieses Bereichs abgebildet. Alle Stempelzahlen eines Bereichs lassen sich paarweise zu Produkten gruppieren, die alle mod m denselben Rest oder dieselbe Stempelzahl ergeben.

Stempelzahlen lassen sich unterteilen in quadratische Reste, Spiegelzahlen quadratischer Reste und nicht quadratische Reste mod m. Für m=30 sind 1 und 19 (15+4) quadratische Reste. Für m=210 sind 1, 121 (105+16) und 151 (256-105), sowie 79 (15+64), 109 (105+4) und 169 (105+64) quadratische Reste (19 nicht mehr!).

Jeder neue Faktor f unterteilt den jeweiligen Stempelzahlenbereich in f-1 Resteklassen (f-1: 2,4,6,10,12,16,18,22,28,...) Alle Stempelzahlen des nächstkleineren Bereichs werden jeder Klasse je einmal zugeteilt. Dadurch finden sich in jeder Klasse genauso viele Zahlen wie der nächstkleinere Bereich an Stempelzahlen enthält! Produkte derselben Klasse ergeben quadratische Reste mod m.

In kleineren Stempel findet sich unter 2*f aufeinander folgenden Zahlen mindestens eine Stempelzahl (f ist der größte Primfaktor des Stempels.)
(Vergleiche hierzu bei Gebhard Glöggler Satz 6 ). Ob die Größe der Stempelzahllücken jedoch auf ein Vielfaches von f beschränkt ist, ist fraglich. In größeren Stempeln überwiegt die Anzahl der zusammengesetzten Zahlen und deshalb können benachbarte Zahlen gestrichen werden und große Lücken entstehen.)

In jedem Stempel ist die erste zusammengesetzt Zahl f_n+1^2, die nächste f_n+1 * f_n+2
(Beispiel 210er Stempel: 11^2 und 11*13 (dann 13^2 und 11*17))
Alle anderen Zahlen bis zu diesen Grenzen sind Primzahlen.

Jede Stempelzahl mit Ausnahme der 2 lässt sich einer der beiden Klassen „Primzahl der Form 4k + 1“ oder „Primzahl der Form 4k + 3“ zuordnen, wobei k eine natürliche Zahl ist. Darüber hinaus hat jede Stempelzahl p > 3 die Form p = 6k + 1 oder p = 6k − 1, wobei k eine natürliche Zahl ist. (In jeder der 4 Klassen gibt es unendlich viele Primzahlen und damit auch Stempelzahlen.)

Primzahlen unterliegen dem Rhythmus der Stempelzahlen, das heißt Stempelzahllücken sind immer auch Primzahlenlücken, aber Primzahlen sind in einem Stempel ungleich verteilt. Die unteren Stempel (einschließlich 210) enthalten ausschließlich oder einen größeren Anteil Primzahlen als die oberen. (Die Dichte der Primzahlen nimmt deutlich schneller ab, als die der Stempelzahlen.

Anzahl und Dichte der Stempelzahlen

Die Anzahl der Stempelzahlen ist das Produkt der um 1 verminderten Faktoren von m.

Wert für 71: D = 0,128 oder jede 7,8 te Zahl ist eine Stempelzahl (von 100 Zahlen ca. 13 Zahlen)!

Bis ca. 106 sind mehr als die Hälfte der Stempelzahlen eines Bereichs Primzahlen.

Beispiele

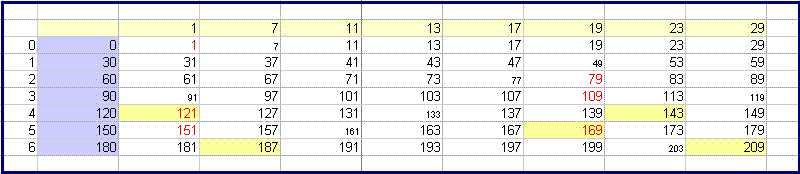
Das folgende Bild stellt die Stempelzahlen des 210er Bereichs dar. Sie sind nach den Stempelzahlen des 30er Bereichs gruppiert. Quadratische Reste sind rot, Produkte mit gelbem Hintergrund markiert. Die zu 210 nicht teilerfremden Vielfachen von 7 sind mit verkleinerter Schriftgröße dargestellt und bilden neue Lücken in diesem Stempel. (Die Vielfachen von 2,3 und 5 sind aufgrund der kleinen ersten Stempel komplett entfallen. 7 und die folgenden Primzahlen bleiben in höheren Stempeln in Kombinationen enthalten (37, 41, 67, 71, ...)

Stempelzahlprodukte

Werden zwei oder mehr Primzahlen miteinander multipliziert, entsteht ein Stempelzahlprodukt der Form:

N = p*q = (x*m + a) * (y*m + b) = m* (x*y*m + a*y + b*x) + a*b

N = p*q = ((2x+1)*m/2 + (a-m/2)) * ((2y+1)*m/2 + (b-m/2))

m ist dabei die Stempelgröße eines kleineren Bereichs.

Sei nun P eine Primzahl im Abstand z*m zu N, dann muss B=(x*y*m + a*y + b*x) teilerfremd zu s = z*m + a*b sein. Da es viele Primzahlen in Abstände z_i*m zu N gibt, existieren viele Stempelzahlen s_i.

Da diese viele Primfaktoren enthalten können und B zu diesen teilerfremd sein muss, ist B meist prim.
Stempelzahlprodukte und Primzahlprodukte lassen sich in 4 Klassen einteilen:
(4k+1)*(6l+1) (4k+1)*(6l-1) (4k+3)*(6l+1) (4k+3)*(6l-1)

Stempelzahlvermutungen

Aus der Struktur der Stempelzahlen kann man Vermutungen zur Struktur der Primzahlen ableiten:

1. Es gibt zu jeder Primzahl p weitere im Abstand einer natürlichen 2er-Potenz. p + 2^n = p_i

Oder dazu äquivalent: Es gibt keine Primzahl p, die nicht durch mindestens eine natürliche Potenz von 2 von einer anderen Primzahl her erreicht werden kann.

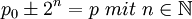
(Diese Vermutung wurde von Cyrix im Matheplanet bewiesen.
Den Beweis dieses Satzes kann man sich durch die oben beschriebene Verschiebung auf andere Stempelzahlen verdeutlichen. Man hat n Möglichkeiten eine Primzahl auf eine andere Stempelzahl zu verschieben und eine davon ist irgendwann sicher prim.)

2. Zu jeder Primzahl existiert eine weitere, so dass gilt: p₁+p₂ = m_i

Anders ausgedrückt: Zu jeder Primzahl existiert ein Stempel, in dem seine Spiegelstempelzahl ebenfalls prim ist.
(Diese Vermutung lässt sich wahrscheinlich ebenso beweisen, wie die erste. Aufgrund der Verteilung der Primzahlen und ihrer Unendlichkeit, muss in der unendlichen Anzahl möglicher Stempel mindestens einer mit dieser Eigenschaft zu finden sein.)

3. Jede Primzahl p kann immer in folgender Form dargestellt werden:
k*s1 - l*s2 =p
Dabei gilt: s1+s2 = mi und k+l= s3
Es lässt sich also eine Stempelzahl s3 so in k und l teilen und mit einer Aufspaltung von mi in zwei weitere Stempelzahlen verbinden, dass die Differenz der Teilprodukte p ergibt.
(Es gilt p= k*mi -s2*(k+l) = k*mi - s2*s3 = k* mi - s4 = s5
Mit dieser Vorschrift erreicht man vermutlich alle Stempelzahlen und damit auch alle Primzahlen.)

4. Jede Primzahl p kann in folgender Form dargestellt werden:
p = k* mi/2 +/- (2^n * p')
wobei k,m,n natürliche Zahlen sind und k ungerade sowie kleiner als der größte Faktor von mi ist.
p' ist 1 oder eine kleine zu mi teilerfremde Primzahl oder hat die Form (2^ l +/- ( mi/2)^ v)
Diese Vermutung folgt direkt aus der oben erwähnten Zerlegung von Stempelzahlen in Summen von Zweierpotenzvielfache von Bereichsmitten. (Bei mi=15 kann mit p'<11 (1, 7) ein 30er Stempel abgedeckt werden. Durch Verschieben werden dann alle Primzahlen erreicht.)
p' kann natürlich ebenfalls wieder genauso zerlegt werden. Primzahlen lassen sich daher als Summen von Zweierpotenzvielfache von Bereichsmitten darstellen.
1007 = 1155 - 4*37 = 1155 - 4*105 + 16*15 + 32
3181 = 211*15 + 16 = 195*15 + 256 = 3*1155-4*105+8+15 +16

Weitere Ideen

Es ist noch zu untersuchen, inwieweit die Stempelzahlen ebenfalls in der Ulam-Spirale charakteristische Linien bilden.
(Hierzu ist auch die etwas andere Darstellung von http://www.numberspiral.com/ heranzuziehen.)

"Schon Euler gab die Formeln n2 + n + 17 und n2 − n + 41 an, die für 0 < n < 16 bzw. 0 < n < 41 Primzahlen liefern. Auch für größere Werte von n liefern die beiden Formeln viele Primzahlen, weil das Ergebnis nie durch Primzahlen p < 17 bzw. p < 41 ganzzahlig teilbar ist. Allgemein gibt es viele solche Formeln an^2 + bn + c, wodurch sich die auffällige Ulam-Spirale erklärt." (Aus: http://de.wikipedia.org/wiki/Primzahl#Formeln_zur_Generierung_von_Primzahlen)
Kann man Formeln der 3. Potenz entwickeln, die drei aufeinander folgende Zahlen miteinander multiplizieren ( n*(n+4)*(n+8) +/- 151 ) und ebenfalls viele Stempelzahlen/Primzahlen liefern?

Fastprimzahlen
Stempelzahlen enthalten Primzahlen und aus mehreren Faktoren zusammengesetzte Zahlen. Die Anzahl der Faktoren der zusammengesetzten Zahlen ist deutlich kleiner als die Anzahl der Faktoren der Stempelgröße, da alle Faktoren des Stempels kleiner sind als der erste mögliche Faktor. Mit 13^3=2197 enthält der 2310er Stempel (n=5) die erste Zahl mit 3 Faktoren. Die Menge der Fastprimzahlen n. Ordnung ist dennoch nicht in den Stempelzahlen enthalten.

Interessant sind die Abstände zwischen Stempelzahlen.
Neben den oben erwähnten Zweierpotenzen sind folgende Abstände häufig:
aus dem 30er Stempel:
10, 20 und 30 selbst,
davon abgeleitet:

k*30 + 2*l*5 mit l<4

und der bekannte Abstand:
k*6 (+/-4)

Zur Größe der Abstände:
Betrachtet man die Abstände von drei aufeinander folgenden Stempelzahlen, so sind diese für kleinere Stempel je kleiner als 2*f (größter Primfaktor) und zusammen bis zu 2*f.
Faktor 19: Stempel: 9699690
old: 6969121 last: 6969139 next: 6969161 olddiff: 18 diff: 22 diffsum: 40
old: 7569721 last: 7569739 next: 7569761 olddiff: 18 diff: 22 diffsum: 40
old: 8766559 last: 8766587 next: 8766599 olddiff: 28 diff: 12 diffsum: 40
old: 9006799 last: 9006827 next: 9006839 olddiff: 28 diff: 12 diffsum: 40
Faktor 23: Stempel: 223092870
old: 19139459 last: 19139489 next: 19139503 olddiff: 30 diff: 14 diffsum: 44
old: 29099047 last: 29099069 next: 29099093 olddiff: 22 diff: 24 diffsum: 46
old: 8302457 last: 8302493 next: 8302499 olddiff: 36 diff: 6 diffsum: 42

Würde man eine Stempelzahl, die mehr als durch den Betrag des größten Faktors von ihrer Nachbarstempelzahl entfernt ist als isoliert bezeichnen,
ergibt sich die Frage, ob es doppelt oder beidseitig isolierte Stempelzahlen innerhalb eines Stempels gibt.

In diesem Zusammenhang steht eine weitere interessante Frage, ob es überhaupt einmal passieren kann, dass nebeneinander liegende Stempelzahlen gleichzeitig beim Übergang zum nächsten Stempel gestrichen werden können. (Starke Vergrößerung von Abständen)

Zu untersuchen ist noch die Summe aller Stempelzahlen bis zur Bereichsmitte:
Bereich Summe
6 1
30 32
210 1248 (1280-32)

Anmerkungen

Interessant ist der Zusammenhang, dass die n-te Wurzel aus der Bereichsgröße des n-ten Stempels mit steigendem n gegen e konvergiert. (siehe Primorial)

Die größten Stempelzahllücken müssten sich immer an den Rändern oder neben Bereichsmitten großer Stempel finden. In der Nähe vieler Primzahllücken finden sich oft Vielfache großer m-Produkte oder deren Hälften (Bereichsmitten). Die Verteilung und Entwicklung von Stempelzahllücken und deren Beziehung zu Primzahlenlücken muss noch untersucht werden.

Das Maximum, über wie viele kleinere Primzahlen eine bestimmte Primzahl durch die Addition von 2er Potenzen erreicht werden kann, ist der ganzzahlige Anteil des Zweierlogarithmus dieser Primzahl. Gibt es Primzahlen, die auf so vielen Wegen erreicht werden können oder ist es immer maximal eins weniger? (19 erreicht mit 17, 11, 3 zum Beispiel 3 von 4)

R sei der Rest eines Stempelzahlprodukts N mod m. Nun gibt es viele Kombinationen von Stempelzahlen des kleineren m-Bereichs a*b, a1*b1, a2*b2, ..., die mod m gleich R sind. Sei Ri = N-ab

und Rz = N - (a-m/2)*(b-m/2) mit

N = p*q = (x*m + a) * (y*m + b) = m* (x*y*m + a*y + b*x) + a*b

Gibt es einen Weg Unterschiede zwischen N-a*b (richtige Kombination) und N-a1*b1 (falsche Kombination) zu finden? Gäbe es einen, könnte man baumartig die Teiler von N ermitteln, ohne dass die Möglichkeiten in diesem Baum zu sehr zunehmen. (siehe Primzahl#Primfaktorzerlegung)

Siehe auch

    * Primfakultät oder Primorial: Primorial
    * Primzahlenzwillinge: Primzahlzwilling
    * Kategorie Primzahlen: Primzahl

Weblinks

    * http://primzahlen.de/
    * http://www.devalco.de/
    * http://beablue.selfip.net/devalco/sieb_des_Ulam.htm
    * http://www.primzahlen.de/files/referent/dk/index.htm
    * http://www.devalco.de/sieb_des_Ulam.htm
    * http://www.luschny.de/math/factorial/Primfakultaet.html
    * http://www.wissenschaft-online.de/abo/ticker/617058
    * http://www.primini.homepage.t-online.de/primgraf.html
    * http://www.g-gloeggler.de/
    * http://www.studentenpilot.de/studieninhalte/onlinelexikon/st/Stempelzahlen/
    * http://www.matheplanet.com/ (Suche Stempelzahlen)
    * http://de.wikipedia.org/wiki/Fastprimzahl 
    * http://primzahlen.de/files/referent/dk/index.htm

Neueste Forschungen zu Primzahlen:
http://www.primzahlen.de/files/home/primality.pdf

Neue Links:
http://primorial-sieve.com/_Sieve_part_1.pdf
http://primorial-sieve.com/_Sieve_part_2.pdf
(Hier werden Listen von weiteren Stempelzahlen geordnet nach den Plätzen eines kleineren Stempels aufgebaut. Es entsteht ein zweidimensionaler Sieb, der besonders für die Suche nach Primzahlenzwillingen hilfreich ist.)

---

(:commentbox:)

---

"Zum Wortbegriff Stempelzahlen. Ich bin selbst noch nicht ganz zufrieden damit, weil eben nicht nur gestempelt wird. Das Streichen ist ja vergleichbar mit dem Sieb des Eratosthenes und im Linkbeitrag redet der Autor von einem konstanten Sieb, den 30er Stempelzahlen.

Nimm die Zahlen 331 und 541 oder 347 und 557 - alles Primzahlen.
Aus der Sicht der Stempelzahlen gehören diese Paare zusammen. Sie sitzen im 210er, im 30er und im 6er Stempel an derselben Stelle (1,1,121 - 5,17,137). Von der Stempelmitte des umschließenden 210er Stempels (315, 525) sind beide 16 oder 32 entfernt.

Ohne den Begriff der Stempelzahlen würde man diese Zusammengehörigkeit nicht so sehen. Sinnvoll wird der Begriff allerdings erst dann, wenn man damit irgendetwas einfacher und eleganter beweisen kann."

Thema Erreichbarkeit von Primzahlen von Stempelzahlen/anderen Primzahlen nur durch Zweierpotenzen:
"Ich hab mir jetzt doch ein kleines Programm geschrieben und gefunden, dass von den ersten 5000 Primzahlen ca 625 nicht von kleineren Primzahlen aus erreicht werden können.
...
Von diesen 625 lassen sich die meisten durch Subtraktion von kleinen 2er Potenzen (unter 20) erreichen. Nur diese neun widersetzten sich bis 2 hoch 30:
3181 11437 21893 42169 43103 43759 44729 47857 48383 "
(Idee der Unterscheidung von Primzahlen in verschiedene Klassen je nach einfacher oder schwieriger Erreichbarkeit über Zweierpotenzen.)

(Klärung: Äquivalenz der Vermutungen, ....)

( Letzte Änderung am 27.11.2012 )